Problem

A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.

Return a deep copy of the list.

• Let $P ={(p \or q), (\neg p \or r), (\neg q \or r), (p \or s)}$, prove that $P\models (r \or s)$ using refutation.

  
  Read more »

Problem

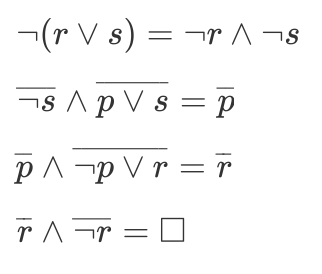
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Examples

1
2
3
4
5
6
7
8
9

Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

1
2
3
4
5
6
7
8
9
10
11
12

Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Problem

Given an array nums and a value val, remove all instances of that value in-place and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

The order of elements can be changed. It doesn’t matter what you leave beyond the new length.

Examples

1
2
3
4

Given nums = [3,2,2,3], val = 3,

Your function should return length = 2, with the first two elements of nums being 2.
It doesn't matter what you leave beyond the returned length.

1
2
3

Given nums = [0,1,2,2,3,0,4,2], val = 2,

Your function should return length = 5, with the first five elements of nums containing 0, 1, 3, 0, and 4.

Problem

Given a sorted array nums, remove the duplicates in-place such that each element appear only once and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Examples

1
2
3
4
5

Given nums = [1,1,2],

Your function should return length = 2, with the first two elements of nums being 1 and 2 respectively.

It doesn't matter what you leave beyond the returned length.

1
2
3
4
5

Given nums = [0,0,1,1,1,2,2,3,3,4],

Your function should return length = 5, with the first five elements of nums being modified to 0, 1, 2, 3, and 4 respectively.

It doesn't matter what values are set beyond the returned length.

Problem

Given a binary search tree and the lowest and highest boundaries as Land R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.

Examples

1
2
3
4
5
6
7
8
9
10
11
12

Input: 
    1
   / \
  0   2

  L = 1
  R = 2

Output: 
    1
      \
       2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Input: 
    3
   / \
  0   4
   \
    2
   /
  1

  L = 1
  R = 3

Output: 
      3
     / 
   2   
  /
 1

Problem

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

Example

1
2
3
4
5
6
7
8
9
10
11
12

Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Problem

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Examples

1
2
3
4
5
6
7

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

1
2

Input: m = 7, n = 3
Output: 28

Problem

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example

1
2
3
4
5
6
7
8
9
10

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

What are the edge cases?

• Some character of the word is not in the board
• You can find the character in the board, but the total number of such caracter is more than the existence number in the board

Problem

Given an n-ary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

Example

We should return its level order traversal:

1
2
3
4
5

[
     [1],
     [3,2,4],
     [5,6]
]