Posted on | Post modified | In

Refutation in Predicate Logic

1
2
3
4
5
6
parent(pam, bob).
parent(tom, bob).
parent(tom, liz).
...
anc(X, Y):- parent(X, Y).
anc(X, Y):- parent(X, Z), anc(Z, Y).

  • Goal G:

    For what values of Q is :- anc(tom, Q) a logical consequence of the above program?

  • Negate the goal G:

    i.e. $\neg G \equiv \forall Q \neg anc(tom, Q).$

  • Consider the clauses in the program $P \cup \neg G$ and apply refutation

    • Note that a program clause written as

      $p(A, B):- q(A, C), r(B, C)$ can be rewritten as

      $\forall A, B, C (p(A, B) \or \neg q(A, C) \or \neg r(B, C))$

    i.e., l.h.s. literal is positive, while all r.h.s. literal are negative

    • Note also that all variables are universally quantified in a clause.

Refutation Examples

Unification

  • Operation done to ‘match’ the goal atom with the head of a clause in the program.
  • Forms the basis for the matching operation we used for Prolog evaluation:
    • f(a, Y) and f(X, b) unify when X=a and Y=b
    • f(a, X) and f(X, b) do not unify
      • f(a, X) = f(X, b) fails in Prolog

Substitutions

  • A substitution is a mapping between variables and values (terms)
    • Denoted by ${x_1/t_1, x_2/t_2, …,x_n/t_n}$ such that
      • $x_i \not= t_i$ ,and
      • $X_i$ and $X_j$ are distinct variables when $i \not = j$
    • The empty substitution is denoted by {} (or $\epsilon$).
    • …

Substitutions and Terms

Compusition of Substitutions

Idempotence

  • A substitution $\theta$ is idempotent iff

Unifiers

  • A substitution $\theta$ is a unifier of two terms s and t if $s\theta$ is identical to $t\theta$

    $\theta$ is a unifier of a set of equations ${s_1=t_1, …, s_n=t_n}$, if for all $i, s_i\theta=t_i\theta$

Equations and Unifiers

  • A set of equations E is in solved form if it is of the form

    ${x_1=t_1,…, x_n=t_n}$ Iff no $x_i$ appears in any $t_j$.

    • Given a set of equations $E={x_1=t_1,…, x_n=t_n}$, the substitution ${x_1/t_1, …, x_n/t_n}$ is an idempotent mug of $E$
    • Two sets of equations $E_1$ and $E_2$ are said to be equivalent iff they have the same set of unifiers.
    • To find the mgu of two terms s and t, try to find a set of equations in solved form that is equivalent to $$

Posted on | Post modified | In

How Good is Your Model?

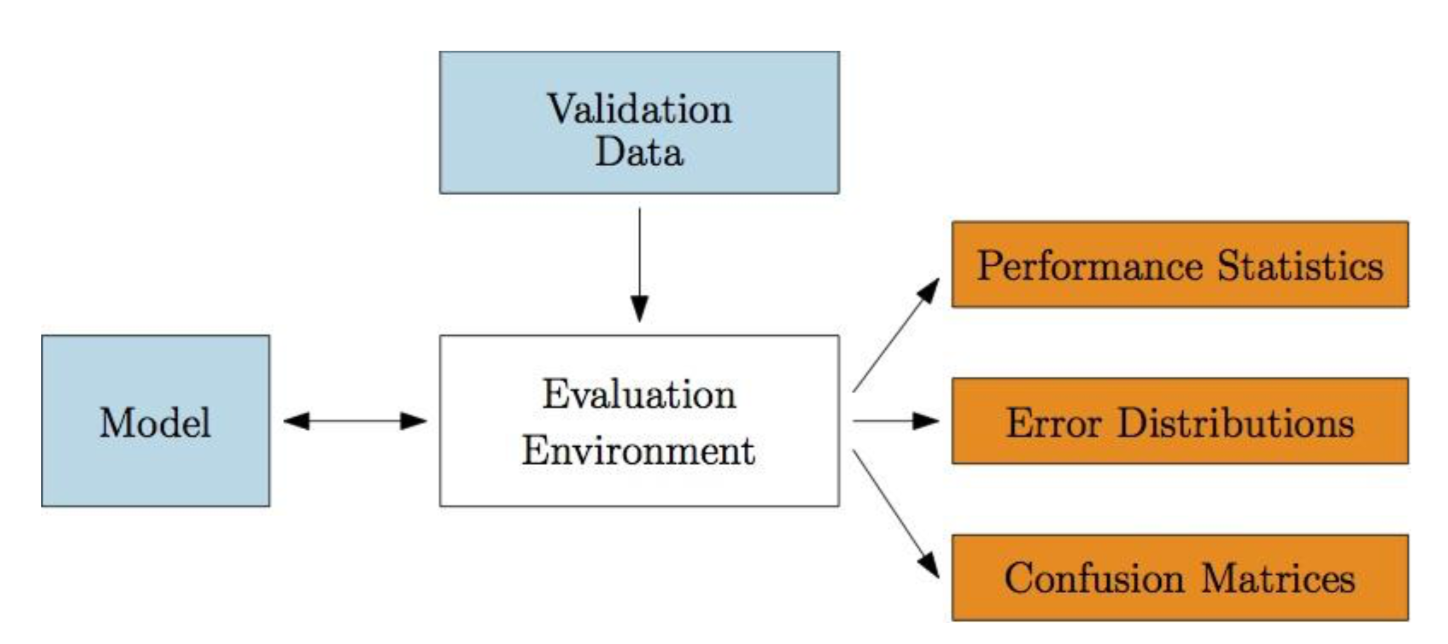
After you train a model. you need to evaluate it on your testing data.

What statistics are most meaningful for:

  • Classification models (which produce labels)
  • Regression models (which produce numerical value predictions)

Evaluating Classifiers

There are four possible outcomes for a binary classifier:

  • True positives (TP) where + is labeled +
  • True negative (TN) where - is labeled -
  • False positives (FP) where - is labeled +
  • False negative (FN) where + is labeled -

Threshold Classifiers

Identifying the best threshold requires deciding on an appropriate evaluation metric.

Accuracy

The accuracy is the ratio of correct predictions over total predictions:

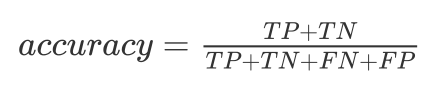
The monkey would randomly guess P/N, with accuracy 50%.

Picking the biggest class yields >= 50%.

Precision

When |P|<<|N|, accuracy is a silly measure. If only 5% of tests say cancer, are we happy with a 50% accurate monkey?

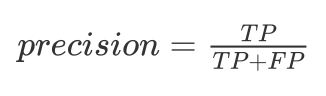
The monkey would achieve 5% precision, as would a sharp always saying cancer.

Recall

In the cancer case, we would tolerate some false positive (scares) to identify real cases:

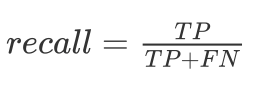
Recall measures being right on positive instances. Saying everyone has cancer gives perfect recall.

F-Score (best single evaluation choice)

To get a meaningful single score balancing precision and recall use F-score:

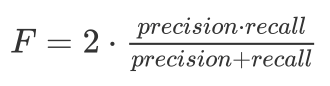
The harmonic mean is always less than/equal to the arithmetic mean, making it tough to get a high F-score.

Take Away Lessons

  • Accuracy is misleading when the class sizes are substantially different.
  • High precision is very hard to achieve in unbalanced class sizes.
  • F-score does the best job of any single statistic, but all four work together to describe the performance of a classifier.

Receiver-Operator Curves (ROC)

Varying the threshold changes recall/precision. Area under ROC is a measure of accuracy.

Evaluating Multiclass Systems

Classification gets harder with more classes.

The confusion matrix shows where the miskates are being made

Confusion Matrix: Dating Documents

What periods are most often confused with each other?

The main diagonal is not exactly where the heaviest weight always is.

Scoring Hard Problems Easier

Too low a classification rate is discouraging and often misleading with multiple classes.

The top-k success rate gives you credit if the right label would have been one of your first k quesses.

It is important to pick k so that real improvements can be recognized.

Summary Statistics: Numerical Error

For numerical values, error is a function of the delta between forecast f and observation o:

  • Absolute error: (f - o)
  • Relative error: (f - o) / o (typically better)

These can be aggregated over many tests:

  • Mean or median squared error
  • Root mean squared error

Evaluation Data

The best way to assess models involve out-of-sample predictions, results on data you never saw (or even better did not exist) when you built the model.

Partitioning the input into training (60%), testing (20%) and evaluation (20%) data works only if you never open evaluation data until the end.

Sin in Evaluation

Formal evaluation metrics reduce models to a few summary statistics. But many problems can be hidden by statistics:

  • Did I mix training and evaluation data?
  • Do I have bugs in my implementation?

Revealing such errors requires understanding the types of errors your model makes.

Building an Evaluation Environment

You need a single-command program to run your model on the evaluation data, and produce plots/reports on its effectiveness.

Input: evaluation data with outcome variables

Embedded: function coding current model

Output: summary statistics and distributions of predictions on data vs. outcome variables

Evaluation Environment Architecture

Designing Good Evaluation Systems

  • Produce error distributions in addition to binary outcomes (how close was your prediction, not just right or wrong).
  • Produce a report with multiple plots / distributions automatically, to read carefully.
  • Output relevant summary statistics about performance to quickly gauge quality.

Error Histograms: Dating Documents

Evaluation Environment: Results Table

The Veil of Ignorance

A joke is not funny the second time because you already know the punchline.

Good performance on data you trained models on is very suspect, because models can easily be overfit.

Out of sample predictions are the key to being honest, if you have enough data/time for them.

Cross-Validation

Often we do not have enough data to separate training and evaluation data.

Train on (k - 1)/k th of the data, evaluate on rest, then repeat, and average.

The win here is that you get a variance as to the accuracy of your model!

The limiting case is leave one out validation.

Amplifying Small Evaluation Sets

  • Create Negative Examples: when positive examples are rare, all others are likely negative
  • Perturb Real Examples: this creates similar but synthetic ones by adding noise
  • Give Partial Credit: score by how far they are from the boundary, not just which side

Probability Similarity Measures

There are several measures of distance between probability distributions.

The KL-Divergence or information gain measures information lost replacing P with Q:

$D_{KL}(P||Q)=\sum_i P(i)ln\frac{P(i)}{Q(i)}$

Entropy is a measure of the information in a distribution.

Blackbox vs. Descriptive Models

Ideally models are descriptive, meaning they explain why they are making their decisions.

Linear regression models are descriptive, because one can see which variables are weighed heaviest.

Neural network models are generally opaque.

Lesson: ‘Distinguishing cars from trucks.’

Deep Learning Models are Blackbox

Deep learning models for computer vision are highly-effective, but opaque as to how they make decisions.

They can be badly fooled by images which would never confuse human observers.

Vocabulary

Posted on | Post modified | In

Logical Consequences of Formulae

  • Recall:

    F is a logical consequence of P

  • Since there are (in general) infinitely many possible interpretations, how can we check if F is a logical consequence of P?

    • Solution:

      choose one ‘canonical‘ model I such that

Definite Clauses

  • A formula of the form $p(t_1, t_2, …, t_n)$ , where $p/n$ is an $n$-ary predicate symbol and $t_i$ are all terms is said to be atomic.

Herbrand Universe

  • Given an alphabet A, the set of all ground terms constructed from the constant and function symbols of A is called the Herbrand Universe of A (denoted by $U_A$).

  • Consider the program:

    1
    2
    p(zero).
    p(s(s(X))) <- p(X).

  • The Herbrand Universe of the program’s alphabet is:

    $U_A={zero, s(zero), s(s(sero)),…}$

Herbrand Universe: Example

  • Consider the ‘relations’ program:

    parent(pam, bob).

    parent(bob, ann).

    parent(tom, bob).

    parent(bob, pat).

    parent(tom, liz).

    parent(pat, jim).

    grandparent(X, Y):-

    ​ parent(X, Z), parent(Z, Y).

  • The Herbrand Universe of the program’s alphabet is:

    $U_A={pam, bob, tom, liz, ann, pat, jim}$

Herbrand Base

  • Given an alphabet A, the set of all ground atomic formulas over A is called the Herbrand Base of A (denoted by $B_A$).

  • Consider the program:

    1
    2
    p(zero).
    p(s(s(X))) <- p(X).

  • The Herbrand Base of the program’s alphabet is:

    $B_A={p(zero), p(s(zero)), p(s(s(zero))),…}$

Herbrand Base: Example

  • Consider the ‘relations’ program:

    parent(pam, bob).

    parent(bob, ann).

    parent(tom, bob).

    parent(bob, pat).

    parent(tom, liz).

    parent(pat, jim).

    grandparent(X, Y):-

    ​ parent(X, Z), parent(Z, Y).

  • The Herbrand Base of the program’s alphabet is:

Herbrand Interpretations and Models

Herbrand Models

  • All Herbrand interpretations of a program give the same ‘meaning’ to the constant and function symbols.
    • Different Herbrand interpretations differ only in the ‘meaning’ they give to the predicate symbols.
  • We often write a Herbrand model simply by listing the subset of the Herbrand base that is true in the model
    • Example: Consider our numbers program, where {p(zero), p(s(s(zero))), p(s(s(s(s(zero))))), …} represents the Herbrand model that treats {…}

Sufficiency of Herbrand Models

  • Let P be a definite program. If I’ is a model of P then I = {} is a Herbrand model of P.
  • (Update lecture slide)

Definite Program Only

  • Let P be a definite program. If I’ is a model of P then I = {$A\in B_P | I’ \imply A$} is a Herbrand model of P.
  • This property holds only for definite programs.
    • Consider P = …
      • There are two Herbrand interpretations:
        • The first is not a model of P since
        • The second is not a model of P since
      • But there are non-Herbrand models, such as I:
        • |I| = N (the set of natural numbers)
        • $a_I = 0$
        • $p_I=$”is odd”

Properties of Herbrand Models

  1. If M is a set of Herbrand Models of a definite program P, then $\cap$M is also a Herbrand Model of P.
  2. For every definite program P there is a unique least model $M_P$ such that:
    • $M_P$ is a Herbrand Model of P and,
    • for every Herbrand Model M, $M_P$
  3. For any definite program, if every Herbrand Model of P is also a Herbrand Model of F, then …
  4. $M_P=$ the set of all ground logical consequences of P.

Least Herbrand Model

  • The least Herbrand model $M_P$of a definite program P is the set of all ground logical consequences of the program.
  • First,
    • By definition of logical consequence, means that has to be in every model of P and hence also in the least Herbrand model.
  • Second,:
    • If … then A is in every Herbrand model of P.
    • But assume there is some model I’
    • By sufficiency of Herbrand models, there is some Herbrand model I such that…
    • Hence A is not in some Herbrand model, and hence is not in $M_P$.

Finding the Least Herbrand Model

  • Immediate consequence operator:
    • Given
    • I’ is said to be the immediate consequence of I.
    • Written as $I’ = T_P(I), T_P$ is called the immediate consequence operator.
    • Consider the sequence:

Computing Mp: Practical Considerations

Posted on | Post modified | In ,

Exploratory Data Analysis

Looking carefully at your data is important:

  • to identify mistakes in collection/processing
  • to find violations of statistical assumptions
  • to observe patterns in the data
  • to make hypothesis

Feeding unvisualized datta to a machine learning algorithm is asking for trouble.

Why Data Visualization?

  • Exploratory data analysis: what does your data really look like?
  • Error detection: did you do something stupid?
  • Presenting what you have learned to others.

A large fraction of the graphs and charts I see are terrible: visualization is harder than it looks.

Ascombe’s Quartet

All four data sets have exactly the same mean variance, correlation, and regression line

=> Plot the Ascombe’s Quartet

Appreciating Art: Which is Better?

Sensible appreciation of art requires developing a particular visual asethetic.

Tufte’s Visualization Aesthetic

Distinguishing good/bad visualizations requires a design aesthetic, and a vocabulary to talk about data representations:

  • Maximize data ink-ratio

    Data-Ink Ratio = $\frac{\text{Data ink}}{\text{Total ink used in graphic}}$

  • Minimize lie factor

    $\frac{\text{(Size of effect in graphic)}}{\text{Size of effect in data}}$

    The fixing a two- or three-dimensional representation by a single parameter yields a lie, because area or volume increase non-proportionally to length.

    Graphical Integrity: Scale Distortion

    Always start bar graphs at zero.

    Always properly label your axes.

    Use continuous scales: linear or labelled.

    Aspect Ratios and Lie Factors

    The steepness of apparent cliffs is a function of aspect ratio. Aim for 45 degree lines or Golden ratio as most interpretable.

  • Minimize chartjunk

    Extraneous visual elements distract from the message the data is trying to tell.

    • Extra dimensionality
    • Uninformative coloring
    • Excessive grids and figurative decoration

    In an exciting graphic, the data tells the story, not the chartjunk

  • Use proper scales and clear labeling

Which Chart to Use

Tabular Data

Tables can advantages over plots:

  • Representation of numerical precision

  • Understandable multivariate visualization:

    each column is a different dimension.

  • Representation of heterogeneous data

  • Compactness for small numbers of points

Always Think this - Can this Table be Improved

Dimensions for Improvement

  • Order rows to invite comparisons.
  • Order rows to highlight importance or pairwise relationships.
  • Right justify uniform-precision numbers.
  • Use emphasis, font, or color to highlight important entries
  • Avoid excessive-length column descriptors.

Line Charts

  • Show data points, not just fits.
  • Line segments show connections, so do not use in categorical data.
  • Connecting points by lines is often chartjunk. Better is usually a trend line or fit with the data points.

Scatter Plots/Multivariate Data

Scatter plots show the values of each point, and are a great way to present 2D data sets.

Higher dimensional datasets are often best projected to 2D, through self-organizing maps or principle component analysis, although can be represented through bubble plots.

Reduce Overplotting by Small Points

Heatmaps Reveal Finer Structure

Color points on the basis of frequency

Bubble Charts for Extra Dimensions

Using color, shape, size, and shading of ‘dots’ enables dot plots to represent additional dimensions.

Bar Plots vs. Pie Charts

Bar plots show the frequency of proportion of categorical variables. Pie charts use more space and are harder to read and compare.

  • Partitioning each bar into pieces yields the stacked bar chart.
  • Pie charts are arguably better for showing percentages of totality, and people do seem to like them, so they may be harmless in small amounts.

Histograms

Histograms (and CDFs) visualize distributions over continuous variables:

  • Histograms are better for displaying peaks, CDFs for showing tails

Histograms: Bin Size/ Count Matters

Frequency vs. Density Histograms

Box and Whisker Plots

Posted on | Post modified | In , , , , , , , , ,

Problem

Given a binary tree

1
2
3
4
5
struct TreeLinkNode {
  TreeLinkNode *left;
  TreeLinkNode *right;
  TreeLinkNode *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Note:

  • You may only use constant extra space.
  • Recursive approach is fine, implicit stack space does not count as extra space for this problem.

Example

Given the following binary tree,

1
2
3
4
5
     1
   /  \
  2    3
 / \    \
4   5    7

After calling your function, the tree should look like:

1
2
3
4
5
     1 -> NULL
   /  \
  2 -> 3 -> NULL
 / \    \
4-> 5 -> 7 -> NULL
Read more »