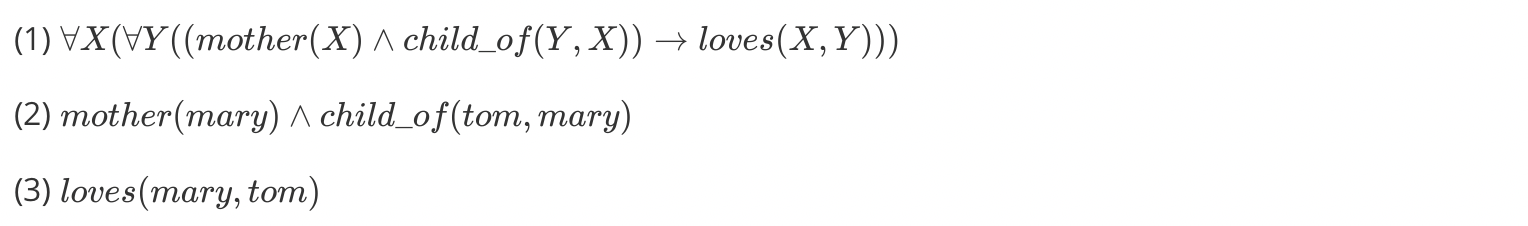The Least Herbrand Model

Definite programs can only express positive knowledge - both facts and rules say which elements of a structure are in a relation, but they do not say when the relations do not hold. Moreover, every definite program has a well defined least model. Intuitively this model reflects all information expressed by the program and nothing more.

Definition (Herbrand universe, Herbrand base)

Let $\bold{A}$ be an alphabet containing at least one constant symbol. The set $\bold{U_A}$ of all ground terms constructed from functors and constants in $\bold{A}$ is called the Herbrand universe of $\bold{A}$. The set $\bold{B_A}$ of all ground, atomic formulas over $\bold{A}$ is called the Herbrand base of $\bold{A}$.

The Herbrand universe and Herbrand base are often defined for a given program.

Example

Consider the following definite program $P$:
$$
odd(s(0)).\
odd(s(s(X)))\leftarrow odd(X).
$$
The program contains one constant (0) and one unary functor (s). Consequently the Herbrand universe looks as follows:
$$
\bold{U_P}={0, s(0), s(s(0)),s(s(s(0))),…}
$$
Since the program contains only one (unary) predicate symbol (odd) it has the following Herbrand base:
$$
\bold{B_P}={odd(0),odd(s(0)), odd(s(s(0))),…}
$$

Example

Consider the following definite program $P$:

Better Regression Models

Proper treatment of variables yie,ds better models:

• Removing outliers
• Fitting nonlinear functions
• Feature/target scaling
• Collapsing highly correlated variables

Outliers and Linear Regression

Because of the quadratic weight of residuals, outlying points can greatly affect the fit.

Identifying outlying points and removing them in a principled way can yield a more robust fit.

Fitting Non-Linear Functions

Linear regression fits lines, not high-order curves.

But we can fit quadratics by creating another variable with the value $x^2$ to our data matrix.

We can fit arbitrary polynomials (including square roots) and exponentials/logarithms by explicitly including the component variables in our data matrix: sqrt(x), log(x), $x^3$, 1/x.

However explicit inclusion of all possible non-linear terms quickly becomes intractable.

Feature Scaling: Z-scores

Features over wide numerical ranges (say national population vs. fractions) require coefficients over wide scales to bring together.
$$
V = c_1 300,000,000 + c_2 0.02
$$
Fixed learning rates (step size) will over/under shoot over such a range, in gradient descent.

Scale the features in your matrix to Z-scores.

Dominance of Power Law Features

Consider a linear model. for years of education, which ranges from 0 to 12+4+5=21
$$
Y=c_1*income + c_2
$$
No such model can gives sensible answers for both my kids and Bill Gates’ kids.

Z-scores of such power law variables don’t help because they are just a linear transformation.

Feature Scaling: Sublinear Functions

An enormous gap between the largest/smallest and median values means no coefficient can use the feature without blowup on big values.

The key is to replace/augment such features x with sublinear functions like log(x) and sqrt(x).

Z-scores of these variables will prove much more meaningful.

Small Coefficients Need Small Targets

Trying to predict income from Z-scored variables will need large coefficients: how can you get to $100,000 from functions of -3 to +3?

If your features are normally distributed, you can only do a good job regressing to a similarly distributed target.

Taking logs of big targets can give better models.

Avoid Highly Correlated Features

Suppose you have two perfectly-correlated features (e.g. height in feet, height in meters).

This is confusing (how should weight be distributed between them) but worse

The rows in the covariance matrix are dependent $\because r_1=c\times r_2, \therefore w=(A^TA)^{-1}A^Tb$ requires inverting a singular matrix.

Punting Highly Correlated Features

Perfectly correlated features provide no additional information for modeling.

Identify them by computing the covariance matrix: either one can go with little loss.

This motivates the problem of dimension reduction: e.g. singular value decomposition, principal component analysis.

Issues with Clsed Form Solution

Definite Clauses

Models and Logical Consequence

Logic Formulas

Example

In declartative form

(i) Every mother loves her children

(ii) Mary is a mother and Tome is Mary’s child

(iii) Mary loves Tom

In formalized form

What is a declarative sentence?

A declarative sentence is a complete expression of natural language which is either true or false, as opposed to e.g. imperative or interrogative sentences (commands and questions). Only declarative sentences can be expressed in predicate logic.

What is the principal idea of logic programming

To describe possibly infinite relations on objects and to apply the programming system in order to draw conclusions.

What does the alphabet of the language of predicate logic consist of?

• variables:

  which will be written as alphanumeric identifiers beginning with capital letters(sometimes subscriped)

• constants:

  which are numerals or alphanumeric identifiers beginning with lowercase letters

• functors:

  which are alphanumeric identifiers beginning with lower-case letters and with an associated arity greater than 0

• predicate symbols:

  which are usually alphanumeric identifiers starting with lowercase letters and with an associated arity greater than or equal to 0

• logical connectives:

  which are conjunction, negation, logical equivalence, implication and disjuction

• quantifiers:

  which are universal and existential

• auxiliary symbols like parentheses and commas

Definition (Term)

Definition (Formulas)

Semantics of Formulas

The meaning of a logic formula is also defined relative to an ‘abstract world’ called an (algebraic) structure and is also either true or false.

To define the meaning of formulas, a formal connection between the language and a structure must be established.

Definition (Interpretation)

Definition (Semantics of terms)

Example

Definition (Semantics of wff’s)

Example

###

Linear Algebra

• It is the language of data science.
• Many machine learning algorithms are best understood through linear algebra.

― Albert Camus |