Linear Algebra
- It is the language of data science.
- Many machine learning algorithms are best understood through linear algebra.
The Power of Linear Algebra
What Can n*m Matrices Represent?

Interpreting Linear Algebraic Formulae
- Concise formulas written as products of matrices provides great power.
- Algebraic substitution coupled with a rich set of identities yields elegant, mechanical ways to manipulate such formulae.
Algebraic Proof: 2 = 1
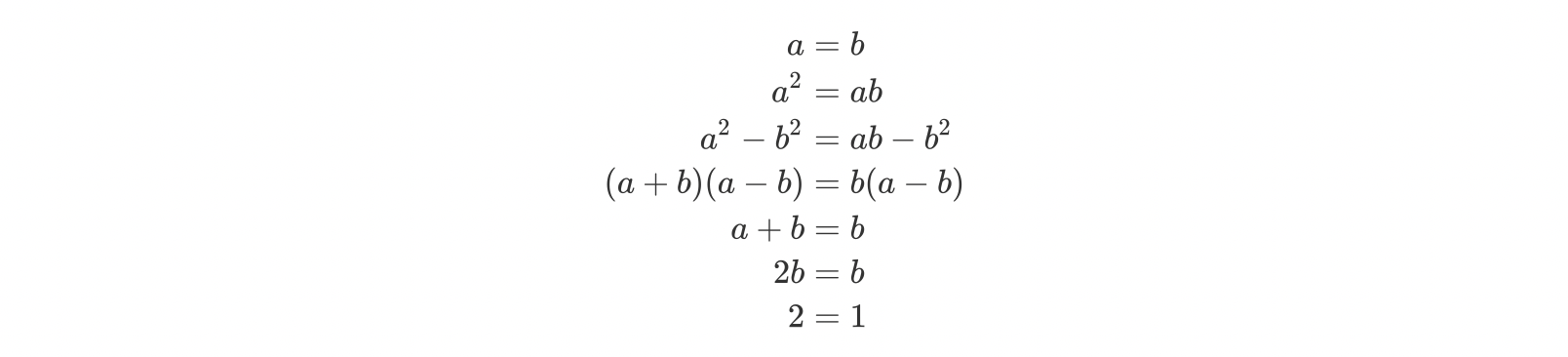
Lessons from the Proof
- Proofs are about ideas, not just algebraic manipulation.
- No idea means no proof.
To understand linear algebra, your goal should be to first validate the simplest interesting case (typically two dimensions) in order to build intuition, and then try to imagine how it might generalize to higher dimensions.
There are always special cases to watch for, like division by zero.
- dimensional mismatches
- Singular (non-invertible) matrices
Geometry and Vectors

Visualizing Matrix Operations
Matrix Addition
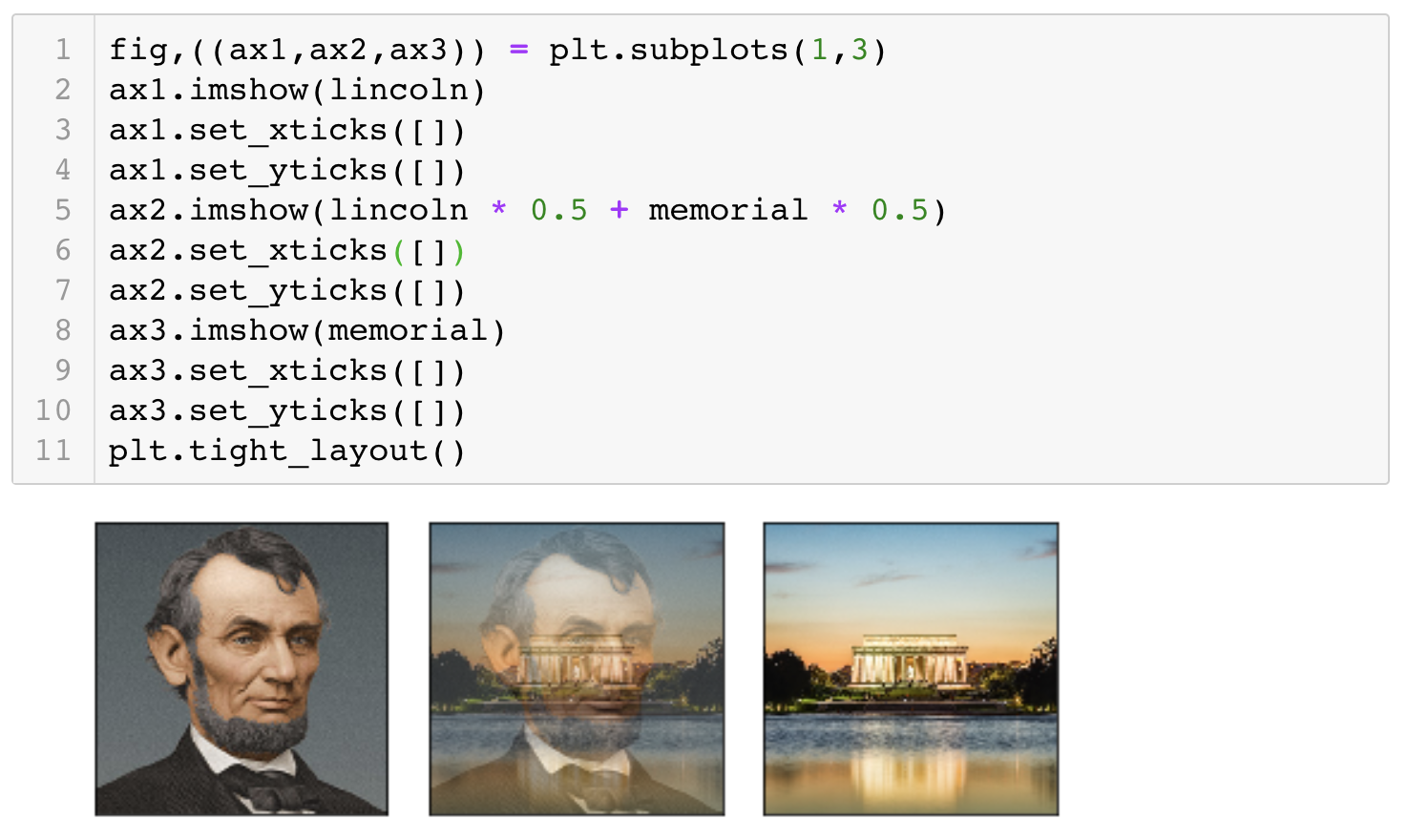
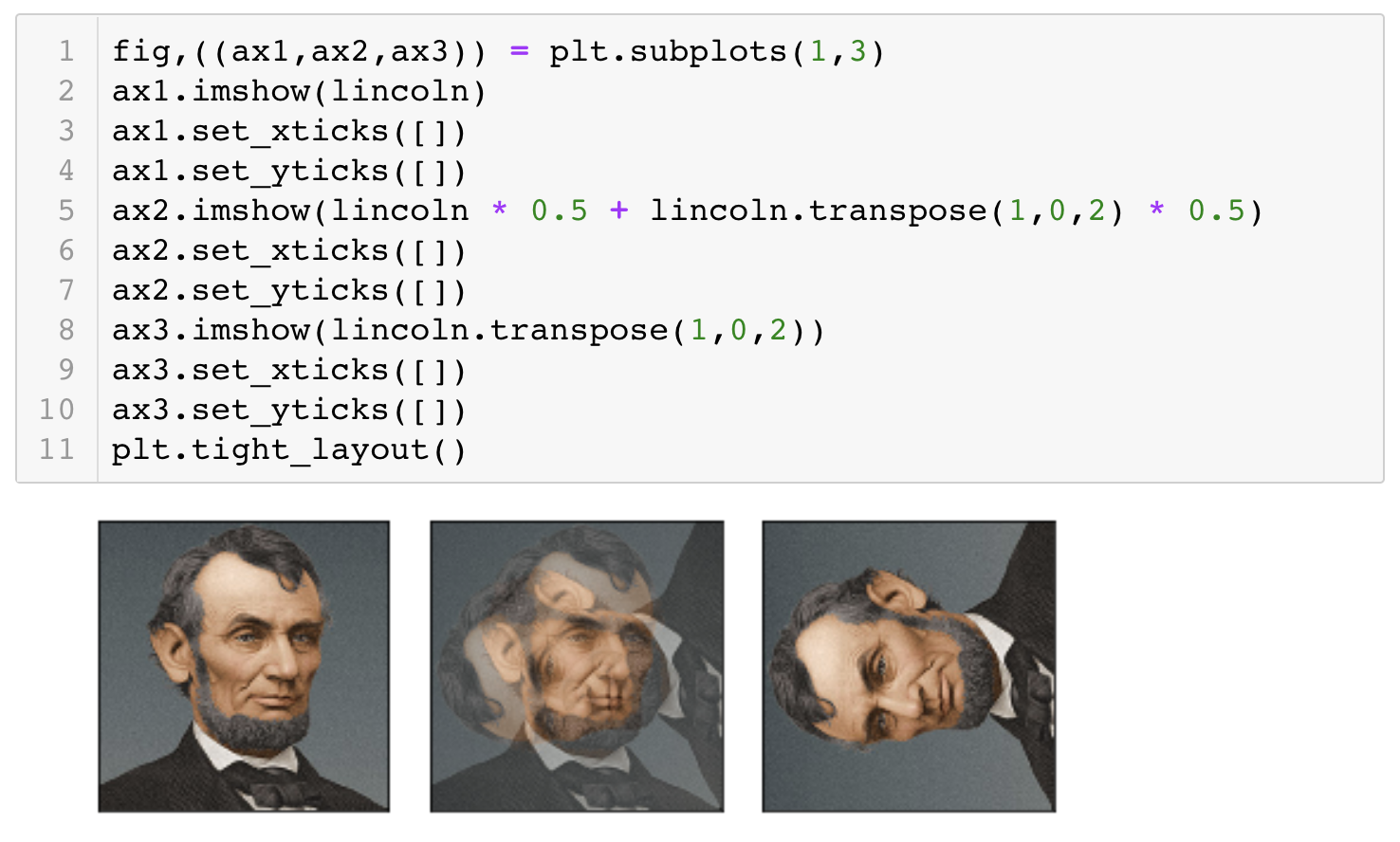
Matrix Multiplication
- Dot products measure how ‘in sync’ the two vectors are, as ion computiong covariance or correlation
- It is associative
- It is not commutative
Covariance Matrices


Matrix Multiplication and Paths
Matrix Multiplication and Permutations
Rotating Points in Space
Identity Matrices and Inversion
Factoring Matrices
Eigenvalues and Eigenvectors
Eigenvalue Decomposition
Reference
[1] The Data Science Design Manual