Introduction to Logic, Logic Programming Concepts and Languages (Part 3)

Posted on | Post modified | In , , , ,

Predicate Calculus or The Logic of Quantified Statements

  • Propositional calculus:

    Analysis of ordinary compound statements

  • Predicate calculus or the Logic of Quantified Statements:

    Symbolic analysis of predicates and quantified statements (forall and exist)

    • P is a predicate symbol

      P stands for ‘is a student at SBU’

      P(x) stands for ‘x is a student at SBU’

    • x is a predicate variable

  • A predicate is a sentence that contains a finite number of variables and becomes a statement when specific values are substituted for the variables.

  • The domain of a predicate variable is the set of all values that may be substituted in place of the variable.

    • Example:

Truth Set of a Predicate

  • If $P(x)$ is a predicate and $x$ has domain $D$, the truth set of $P(x), {x \in D | P(x)}$, is the set of all elements of $D$ that make $P(x)$ true when they are substituted for $x$.

Quantifiers

Quantifiers are words that refer to quantities (‘some’ or ‘all’) and tell for how many elements a given predicate is true.

The Universal Quantifier: for all

The Existential Quantifier: exist

Universal Conditional Statements

Implicit Quantification

Negations of Quantified Statements

Vacuous Truth of Universal Statements

Variants of Universal Conditional Statements

Necessary and Sufficient Conditions

  • Necessary condition:

  • Sufficient condition:

  • Examples:

    • There is a person supervising every detail of the production process

      What is the meaning?

      • There is one single person who supervises all the details of the production process

        or

      • For any particular production detail, there is a person who supervises that detail, but there might be different supervisors for different details

      Natural language is ambiguous

      Logic is clear

Statements with Multiple Quantifiers

Quantifiers are performed in the order in which the quantifiers occurs.

Validity of Arguments with Quantified Statements

An argument form is valid, if and only if, for any particular predicates substituted for the predicate symbols in the premises if the resulting premise statements are all true, then the conclusion is also true.

Universal Transitivity

  • Formal Version

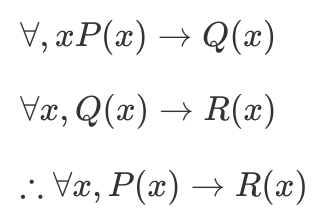
  • Informal Version

Vocabularies

Reference

Lecture Slide: Introduction to Logic, Logic Programming Concepts and Languages