Introduction to Logic, Logic Programming Concepts and Languages (Part 2)

Posted on | Post modified | In , , ,

Logical Equivalence

The properties of the logical connectives can also be exploited to simplify the notations.

  • If two formulas evaluate to the same truth value in all situations, so that their truth tables are the same, they are said to be logically equivalent
  • We write $p \equiv q$ to indicate that two formulas p and q are logically equivalent
  • If two formulas are logically equivalent, their syntax may be different, but their semantics is the same.
  • The logical equivalence of two formulas can be established by inspecting the associated truth tables.
  • Substituting logically inequivalent formulas is the source of most real-world reasoning errors

Some Logical Equivalences

  • Tautologies and Contradictions
    • A tautology is a formula that is always true, no matter which truth values we assign to its variables.
    • A contradiction is a formula that is always false.
    • If p is a tautology (contradiction) then not p is a contradiction (tautology).

Logical Consequence

  • We say that p logically implies q, or that q is a logical consequence of p, if q is true whenever p is true.
  • Note that logical consequence is a weaker condition than logical equivalence.

Logical Arguments

  • An argument (form) is a (finite) sequence of statements (forms), usually written as follows:

    p1

    …

    pn

    Therefore q

  • We call p1, …, pn the premises (or assumptions or hypotheses) and q the conclusion, of the argument.

  • We read:

    p1, p2, ..., pn, therefore q or

    from premises p1, p2, ..., pn, infer conclusion q

  • Argument forms are also called inference rules

  • An inference rule is said to be valid, or (logically) sound, if it is the case that, for each truth valuation, if all the premises true, then the conclusion is also true.

Theorem:

An inference rule is valid if, and only if, the conditional p1 and p2 and … and pn implies q is a tautology.

  • An argument form consisting of two premises and a conclusion is called a syllogism

Determining Validity or Invalidity

Testing an Argument Form for validity

  1. Identify the premises and conclusion of the argument form.

  2. Construct a truth table showing the truth values of all the premises and the conclusion.

  3. A row of the truth table in which all the premises are true is called a critical row.

    • If there is a critical row in which the conclusion is false, then the argument form is invalid.

    • If the conclusion in every critical row is true, then the argument form is valid.

Modus Ponens (Method of Affirming)

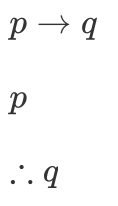
Modus Tollens (Method of Denying)

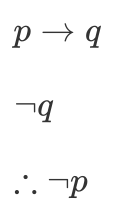
  • Modus tollens is valid because:
    • modus ponens is valid and the fact that a conditional statement is logically equivalent to its contrapositive, OR
    • it can be established formally by using a truth table

Recognizing Modus Ponens and Modus Tollens

Example:

If there are more pigeons than there are pigeonholes, then at least two pigeons roost in the same hole.
There are more pigeons than there are pigeonholes.
Therefore, at least two pigeons roost in the same hole. (by modus ponens)

If 870,232 is divisible by 6, then it is divisible by 3.
870,232 is not divisible by 3.
Therefore 870,232 is not divisible by 6. (by modus tollens)

Other Rules of Inference

  • Generalization

  • Specialization

  • Elimination

    • If we have only two possibilities and we can rule one out, the other must be the case

  • Transitivity

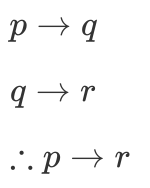
Proof Techniques

Proof by Contradiction:

Vocabularies

Reference

Lecture Slide: Introduction to Logic, Logic Programming Concepts and Languages