The Data Science Analysis Pipeline
Ask an interesting question
What is the scientific goal?
What would you do if you had the data?
What do you want to predict or estimate?
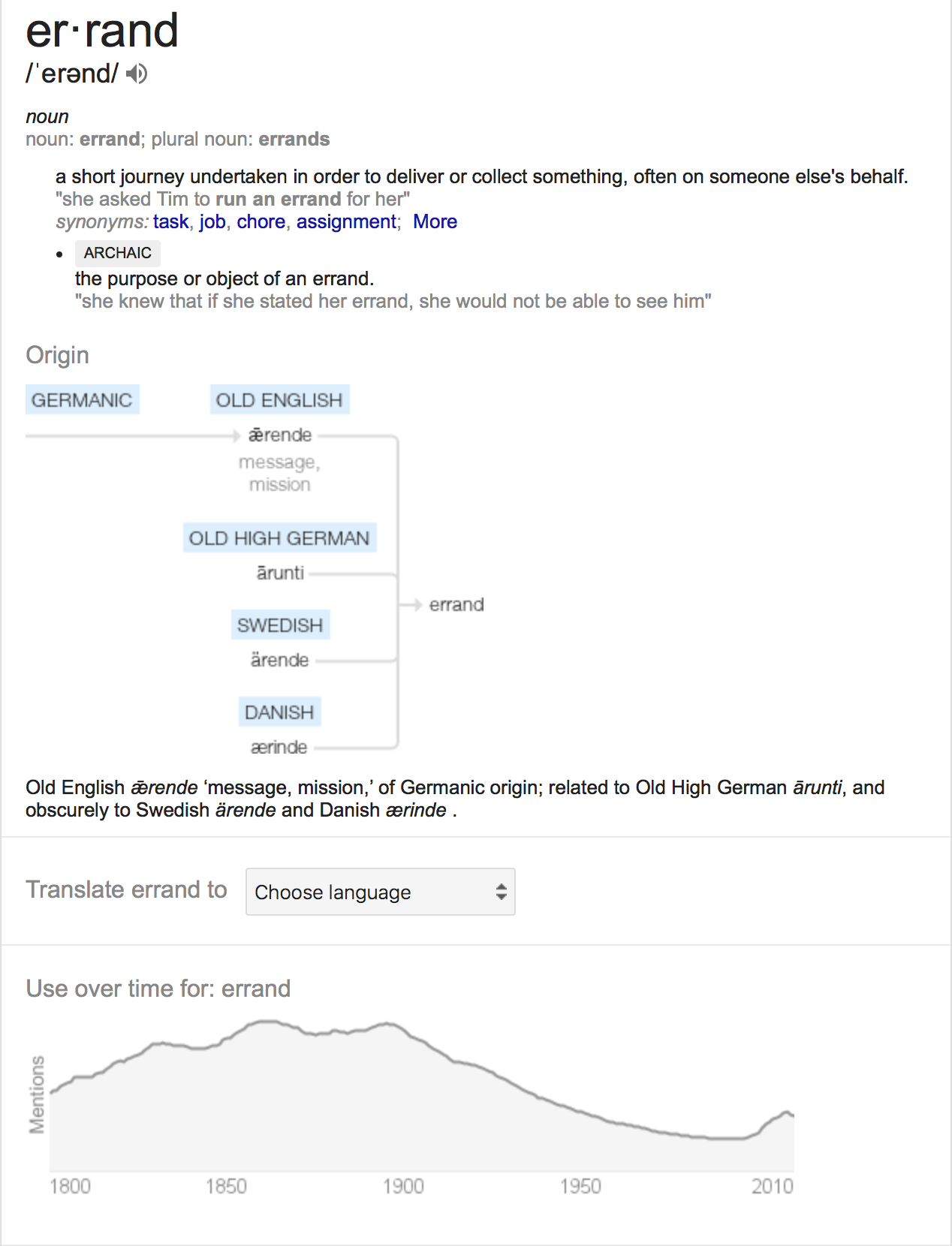
Get the data
How were the data sampled?
Which data are relevant?
Are there privacy issues?
Explore the data
Plot the data.
Are there anomalies?
Are there patterns?
Model the data
Build a model.
Fit the model.
Validate the model.
Communicate and visualize the results
What did we learn?
Do the results make sense?
Can we tell a story?
Modeling is the process of encapsulating information into a tool which can make forecases/predictions.
The key steps are building, fitting, and validating the model.
Philosophies of Modeling
We need to think in some fundamental ways about modeling to build them in sensible ways.
Occam’s razor
When presented with competing hypotheses to solve a problem, one should select the solution with the fewest assumptions.
With respect to modeling, this often means minimizing the parameter count in a model.
Machine learning methods like LASSO/ridge regression employ penalty functions to minimize features, but also do a ‘sniff test’.
Bias-Variance tradeoffs
Bias is error from incorrect assumptions built into the model, such as restricting an interpolating function to be linear instead of a higher-order curve
Errors of bias produce underfit models.
They do not fit the training data as tightly as possible.
Models that perform lousy on both training and testing data are underfit.
Variance is error from sensitivity to fluctuations in the training set. If our training set contains sampling or measurement error, this noise introduces variance into the resulting model
Errors of variance result in overfit models.
Models that do much better on testing data than training data are overfit.
Models based on first-principles or assumptions are likely to suffer from bias
Data-driven models are in greater danger of overfitting
Nate Silver: The Signal and Noise
Principles of Nate Silver:
Think probabilistically
Demanding a single deterministic ‘prediction’ from a model is a fool’s errand.
Good forecasting models generally produce a probability distribution over all possible events.
Good models do better than baseline models, but you could get rich predicting if the stock market goes up/down with p > 0.55.
Properties of Probabilities
- They sum to 1
- They are never negative
- Rare events do not get probabilities of zero
Probabilities are a measure of humility in the accuracy of the model, and the uncertainty of a complex world.
Models must be honest in what they do/don’t know.
Scores to Probabilities
The logit function maps scores into probabilities using only one parameter.
Summing up the ‘probabilities’ over all events s defines the constant 1/s to multiply each so they sum up to 1.
Change your forecast in response to new information
A model is live if it is continually updating predictions in response to new information.
Dynamically-changing forecasts provide excellent opportunities to evaluate your model.
Do they ultimately converge on the right answer?
Does it display past forecasts so the user can judge the consistency of the model?
Does the model retrain on fresher data?
Look for consensus
A good forecast comes from multiple distinct sources of evidence.
Ideally, multiple models should be built, each trying to predict the same thing in different ways.
- Are there competing forecasts you can compare to, e.g. prediction markets?
- What do your baseline models say?
- Do you have multiple models which use different approaches to making the forecast?
Boosting is a machine learning technique which explicitly combines an ensemble of classifier.
Employ Bayesian reasoning
Bayes’ theorem lets us update our confidence in an event in response to fresh evidence.
When stated as $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$ , it provides a way to calculate how the probability of event A changes in response to new evidence B.
Bayesian reasoning relfects how a prior probability P(A) is updated to given the posterior probability P(A|B) in the face of a new observation B according to the ratio of the likelihood P(B|A) and the marginal probability P(B).
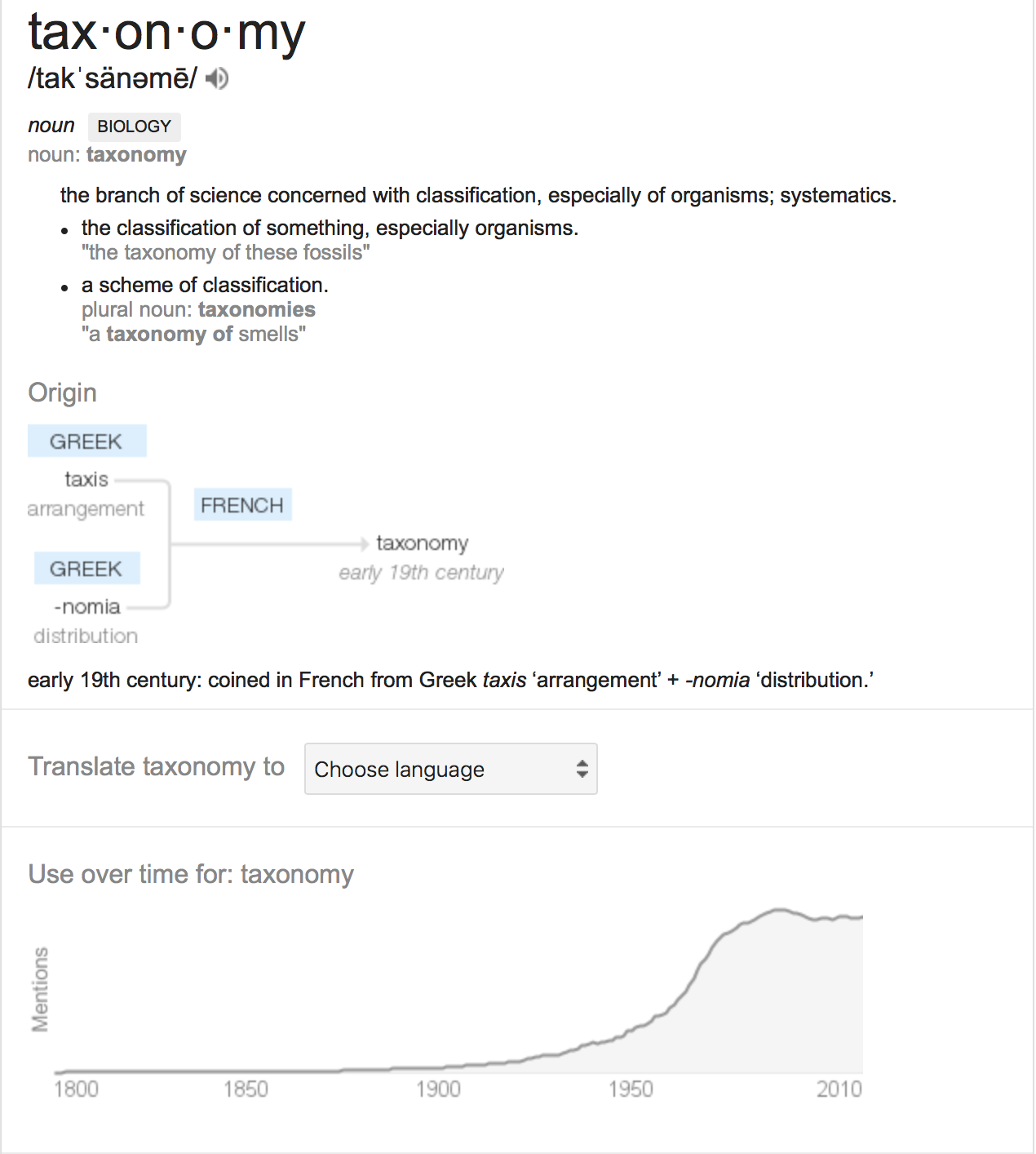
A Taxonomy of Models
Modeling Methodologies
First-principle models
Based on a belief of how the system under investigation really works. It might be a theretical explanation, a discrete event simulation, or seat-of-the-pants reasoning from an understanding of the domain
Data-driven models
Based on observed correlations between input parameters and outcome variables.
Good models are typically a mixture of both.
Models have different properties inherent in how they are constructed:
Linear vs. Non-Linear Models
Discrete vs. Continuous Models
Discrete models manipulate discrete entities.
Representative are discrete-event simulations using randomized (Monte Carlo) methods.
Continuous models forecast numerical quantities over reals.
They can employ the full weight of classical mathematics: calculus, algebrea, geometry, etc.
Blackbox vs. Descriptive Models
Stochastic vs. Deterministic Models
Flat vs. Hierarchical Models
[TODO]
General vs. Ad Hoc Models
Machine learning models for classification and regression are general, meaning they employ no problem-specific ideas, only specific data.
Ad hoc models are built using domain-specific knowledge to guide their structure and design.
Steps to Build Effiective Models
- Identify the best output type for your model, likely a probability distribution.
- Develop reasonable baseline models.
- Identify the most important levels to build submodels around.
- Test models with out-of-sample predictions.
Baseline Models
A broken clock is right twice a day.
The first step to assess whether your model is any good is to build baseline models: the simplest reasonable models that produce answers we can compare against.
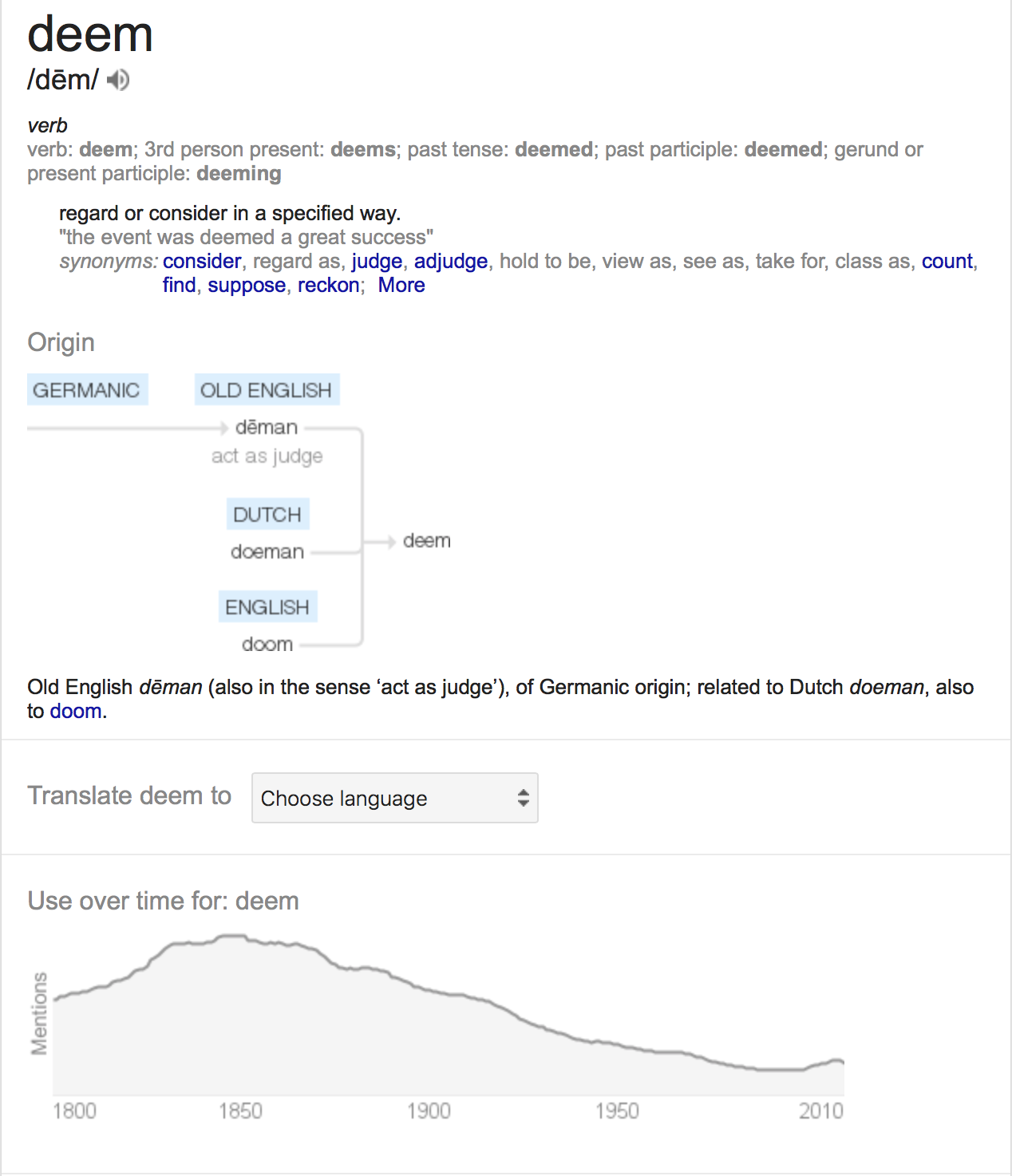
Only after you decisively beat your baselines can your models be deemed effective.
There are two common tasks for data science models: classification and value prediction.
Representative Baseline Models for Classification Tasks
- Uniform or random selection among labels
- The most common label appearing in the training data
- The most accurate single-feature model
- Same label as the previous point in time
- Rule of thumb heuristics
- Sombody else’s model
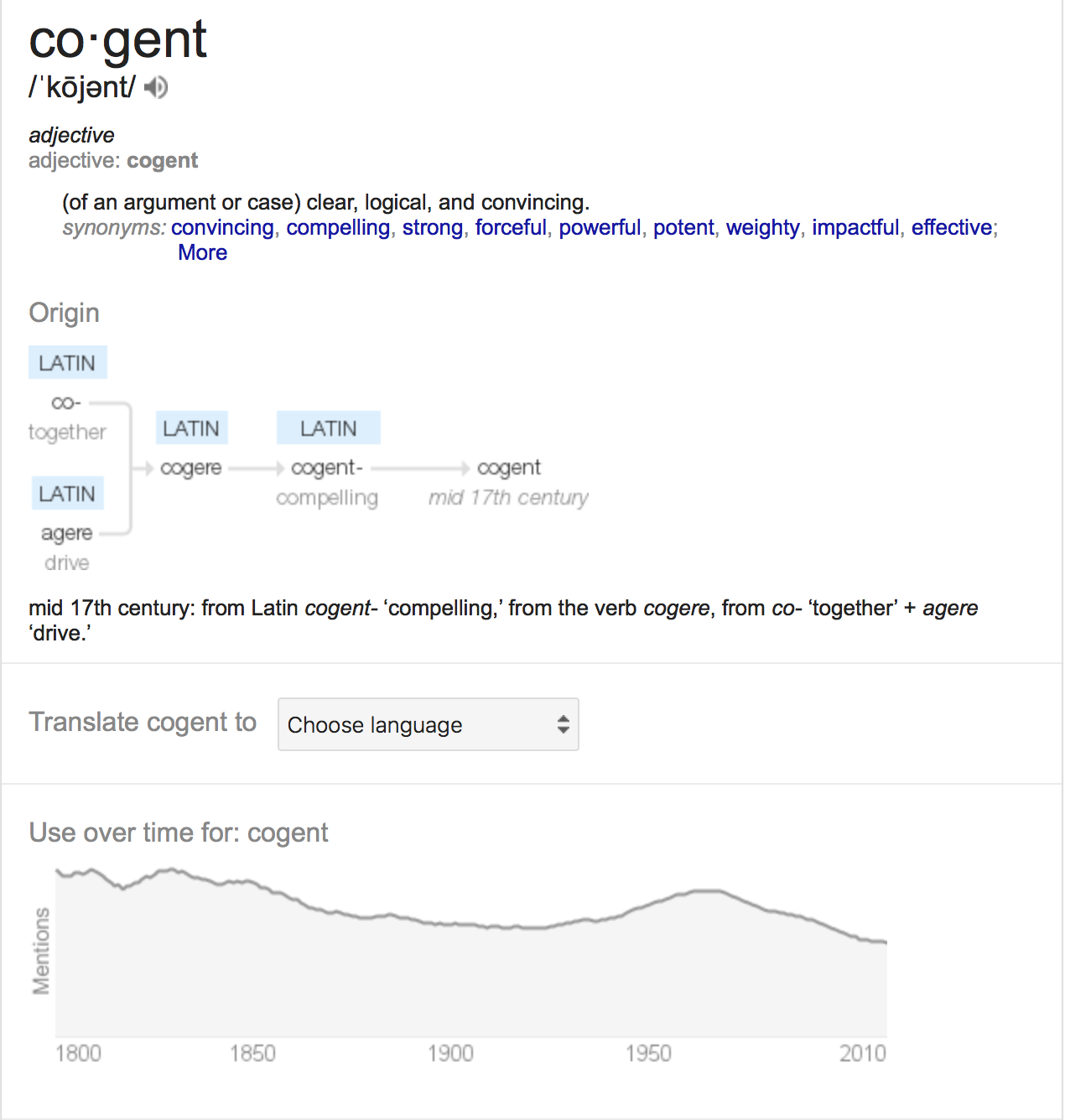
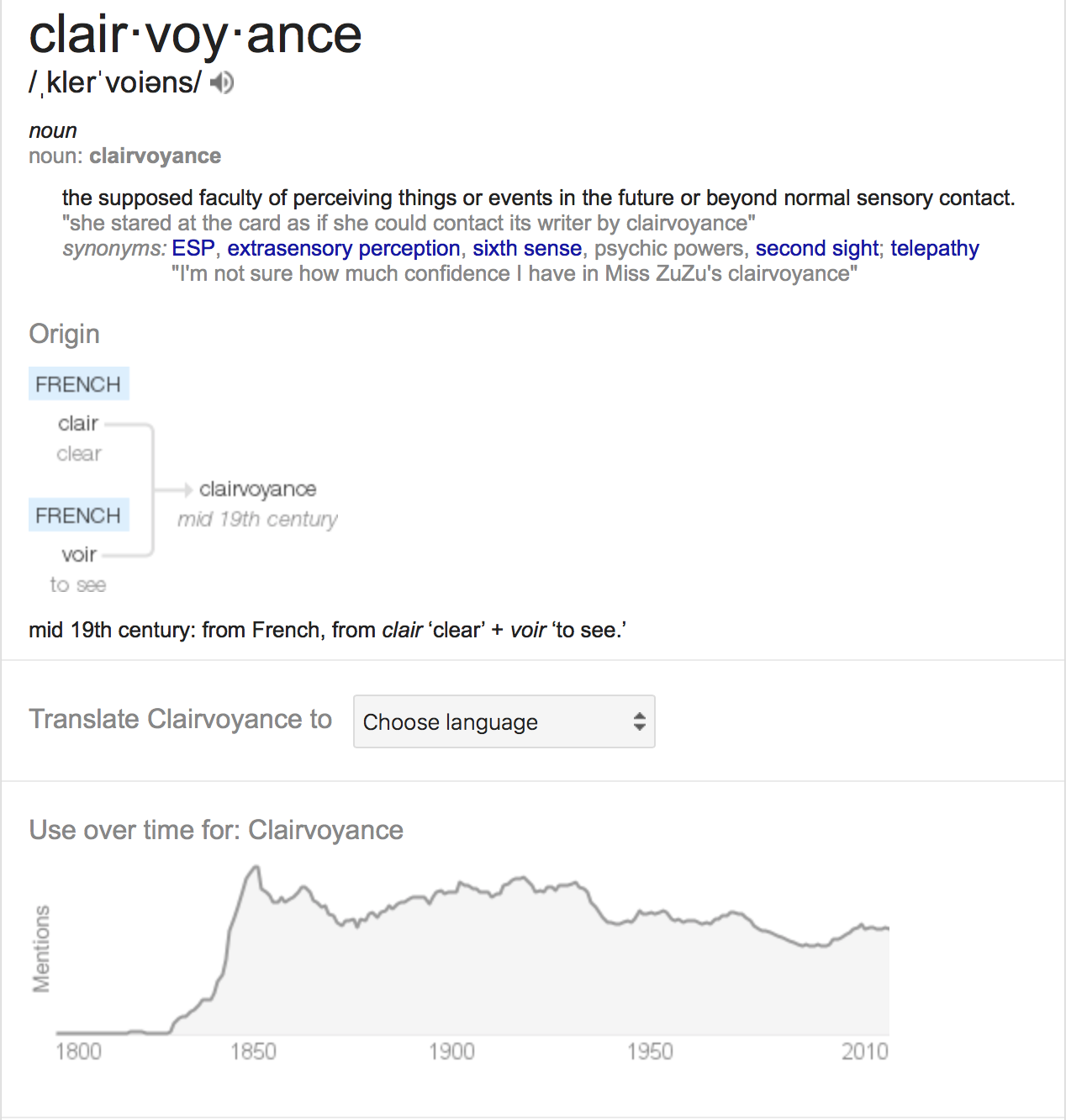
- Clairvoyance
Baseline models must be fair: they should be simple but not stupid.
Baseline Models for Value Prediction
In value prediction problems, we are given a collection of feature-value pairs (fi, vi) to use to train a function F such that F(vi) = vi.
- Mean or median
- Linear regression
- Value of the previous point in time
Evaluating Models
Evaluation Environments
Simulation Models
Vocabularies